What is FaSTrack?
FaSTrack is a tool that is used in conjunction with any model-based motion planner to provide safety guarantees while planning and executing trajectories in real time. FaSTrack allows the planner to find trajectories using simple and easily computed planning models; this allows for the planner to operate in real time. To guarantee safety, a tracking error bound is precomputed to provide bounds on the largest deviation possible between the simple planner and the more complicated autonomous system.
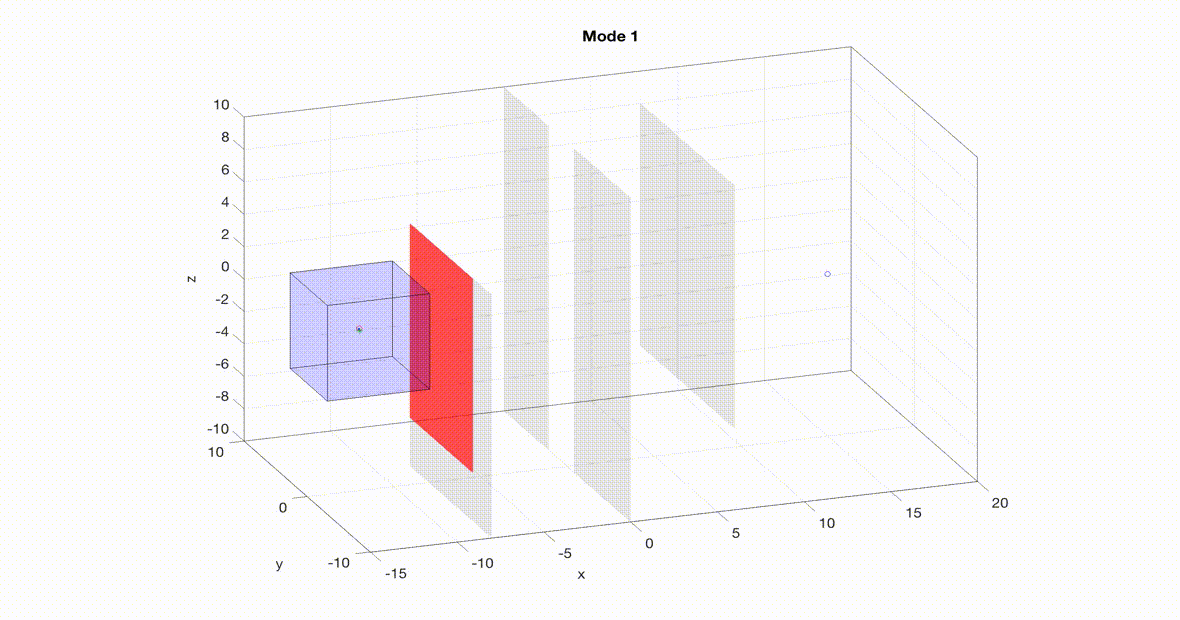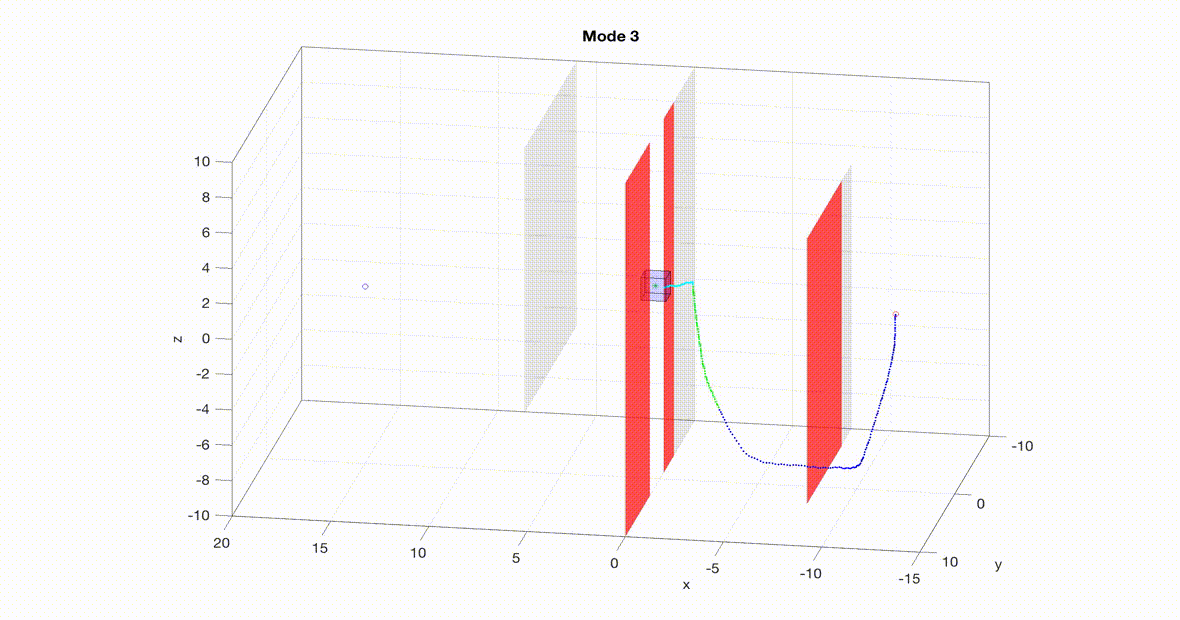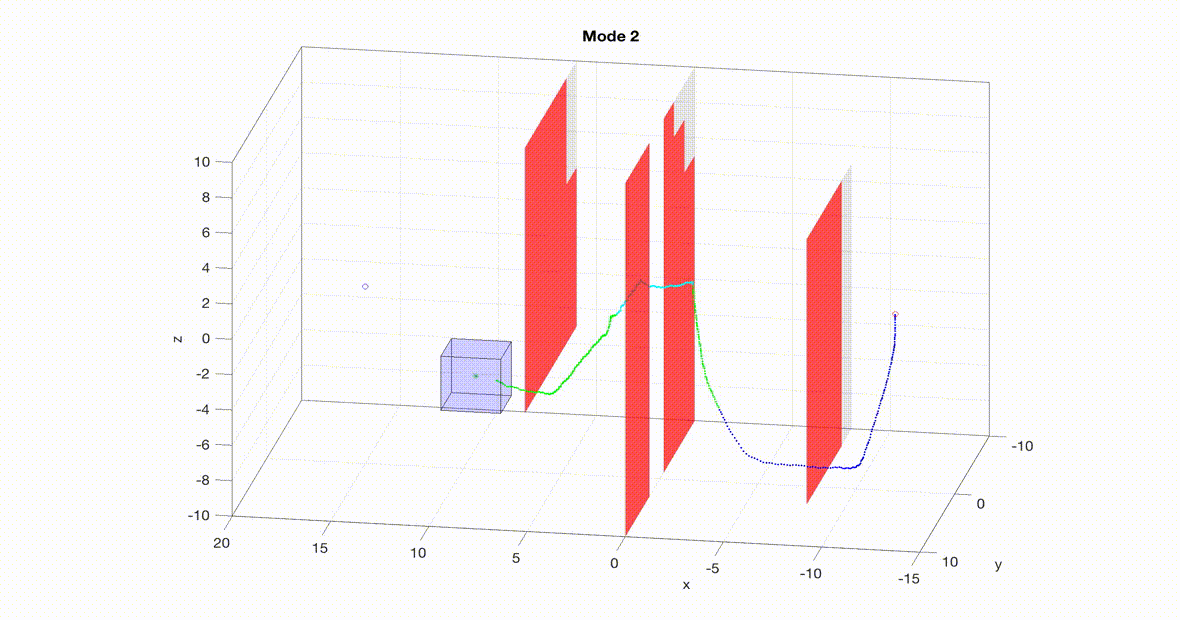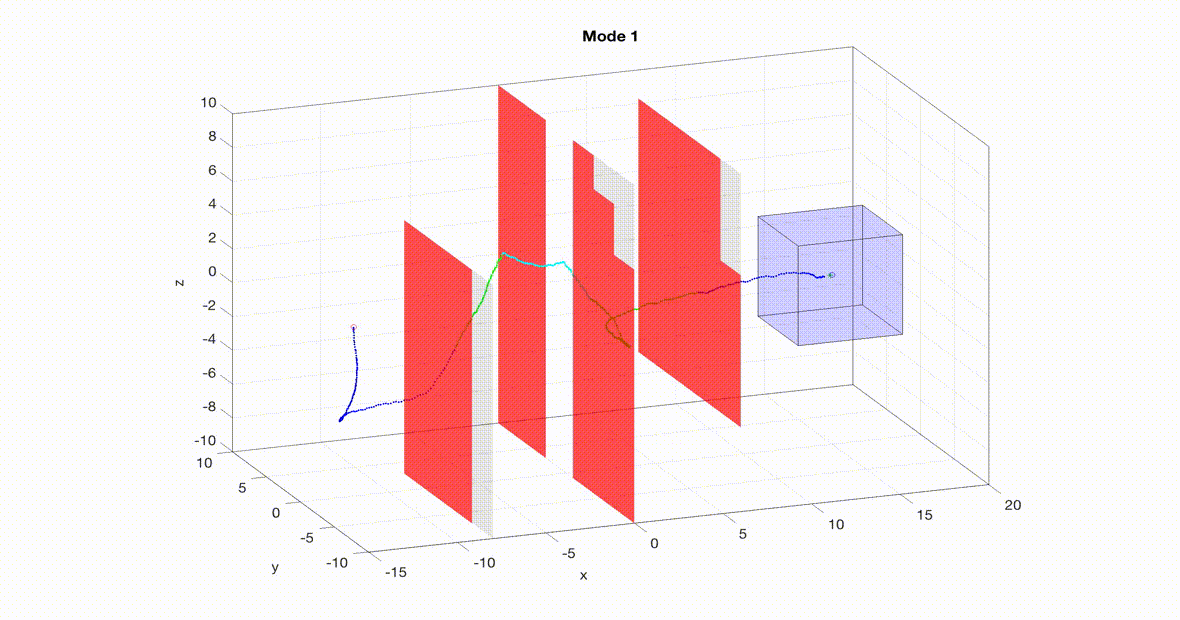
A nonlinear, ten-dimensional quadrotor simulation navigating an obstacle course in real-time with guaranteed safety. The planner is a 3D RRT planner with a tracking error bound (think safety bubble) based on the speed of the planner. Note that the planner mode changes throughout the course to trade off speed with maneuverability. As the planner senses its environment the local obstacles turn red and the planner replans.
The Thorough Explanation
On the left we have a high-dimensional vehicle moving through an obstacle course to a goal. Computing the optimal safe trajectory is a slow and sometimes intractable task, and replanning is nearly impossible. In the center we simplify our model of the vehicle (in this case assuming it can move in straight lines connected at points). This allows us to plan very quickly, but when we execute the planned trajectory we may find that we cannot actually follow the path exactly, and end up crashing. On the right we have our proposal: plan using the simplified model, but precompute a tracking error bound that captures all potential deviations of the trajectory due to model mismatch.
Guaranteed safe real-time motion planning is a difficult challenge, particularly for systems with complicated dynamics, external disturbances (like wind), and a priori unknown environments. Using the reachability techniques developed in our lab, safe motion planning can be accomplished for decomposable and/or low dimensional systems; however even in these situations our techniques can't process safe trajectories for systems of more than about two dimensions in real time. For real life systems like cars, planes, and quadrotors, fast planning is intractable. On the other hand, motion planners like rapidly-exploring random trees (RRT) or model-predictive control (MPC) can plan in real time by using simplified models of system dynamics, which sacrifice guarantees of safety and feasibility. Our tool allows users to implement a fast motion planner for simplified dynamics while maintaining safety by providing a precomputed bound on the maximum possible tracking error between the planner and the autonomous system. This precomputation also results in an optimal control look-up table which provides the optimal control for the autonomous system to pursue the online planner in real time.
Offline Precomputation
We precompute this bound by viewing the problem as a pursuit-evasion game between a planner and a tracker. The planner uses a simplified model of the system that is necessary for fast planning; the tracker uses a model of the true autonomous system. We assume that the tracker is always pursuing the planner; in other words, the autonomous system is always trying to follow the planner. We want to know what the maximum relative distance (i.e. maximum tracking error) could be in the worst case scenario: when the planner is actively attempting to evade the tracker. If we have an upper limit on this bound then we know the maximum tracking error that can occur during the online planning.
To solve this pursuit-evasion game we first find the relative dynamics between the two systems. We then set a cost function as the distance of the tracking system to the planning system. The tracking system will try to minimize this cost/distance, and the planning system will do the opposite. While evolving these optimal trajectories over time, we capture the highest cost that occurs of the time period. If the tracking system can always eventually reach the planning system, this cost converges to a fixed cost for all time. That converged cost is the tracking error bound. For a more thorough explanation of the optimization, please see our paper.
The value function initializes at the cost function (normed distance to the origin) and evolves over time to convergence
An example of a 3D set at the slice V = 0.75 meters of the value function. We can think of this as a "candidate" tracking error bound. As the set evolves we see the initial states we must start in (purple) in order to stay within the desired bound (blue)
Online Planning
In the online phase, we sense obstacles within a given radius and expand these obstacles by the tracking error bound through minkowski addition. Using these padded obstacles, the planner decides the next desired state. Based on the relative state between the tracker and planner, the optimal control is determined from the look-up table. The autonomous system executes the optimal control, and the process repeats. For more details, please see our paper.
Demonstrations
Simulations
Two MATLAB simulations can be seen below. On the left is a simulation of a 10D quadrotor model pursuing a 3D planner using RRT (Rapidly-Exploring Random Trees). The planner (green dot) uses RRT to find a path towards the goal. The quadrotor (blue) then uses the tracking controller (i.e. the optimal error-feedback look-up table) to pursue the planner. As new obstacles are sensed (turning red), the planner re-plans. Even when the planner takes sharp turns, the tracker remains within the tracking error bound (blue box). For more details on this implementation please see our paper.
Note: even though RRT doesn't use a model of the system to plan paths, we can interpret its paths as a 3D point mass model moving at a fixed speed. So even though RRT isn't a model-based planner it still works for FaSTrack!
On the right we have a MATLAB Simulation of a 5D plane model tracking a 3D planner using Fast Sweeping Method. Note here that we are visualizing the augmented obstacles instead of visualizing the error bound around the planner.
Hardware
A hardware demo (and a C++/ROS simulation demo) can be seen in our ICRA video submission for Meta-FaSTrack.
Challenges & Next Steps
Conservativeness of precomputation
We acquire this guaranteed tracking error bound from FaSTrack by assuming an adversarial relationship between the tracker and planner. This means we expect the planner to be actively avoiding the tracker. In reality, during online navigation the planner is not even aware of the tracker and is simply trying to find a path to the goal, essentially ensuring that our error bound is overly conservative. We have two ideas for dealing with this. The first (and simpler) idea was inspired by cognitive science research on humans regarding our ability to switch between fast and slow modes of thinking. Trying to mimic this meta-planning in our algorithm resulted in Meta-FaSTrack, where a meta-planner switches between fast and slow planning based on the local environment while maintaining safety (see Figure on the right for illustration). Here we are still assuming an adversarial relationship, but we switch between relationships based on our needs. For more information please see our paper on the project. The second idea that we are exploring is on contract-based methods of cooperation between the tracker and planner to remove this adversarial assumption.
Outdoor demonstration
We are working with members of Professor Shankar Sastry and Dr. Allen Yang's group to integrate our C++/ROS code for FaSTrack with onboard sensing and state estimation. We will then test everything outdoors on a Matrice 600 UAV!
Modularity with respect to planners
FaSTrack is designed to be modular with respect to path and trajectory planners. We are looking into integrating the Open Motion Planning Library (OMPL) into our codebase to easily select the desired planner. We are also working on meta-planning algorithms that allow for switching between planners types (for example, switching from RRT to Model-Predictive Control).
Curse of dimensionality in precomputation
In the offline computation we solve our differential game using level set methods and Hamilton-Jacobi reachability analysis. This involves discretizing the state space and solving over a grid corresponding to the number of states in the dynamic system. This discretization causes computational complexity to rise exponentially with respect to system dimension, resulting in the "curse of dimensionality." In FaSTrack, relative dynamics of more than ~4 states are intractable to solve directly. To deal with this we use our Reachability Decomposition work (note how the 10D MATLAB example has a square tracking error bound. This is due to the decomposition). We are also exploring methods to learn the converged value function for the precomputation using neural networks.
Multi-agent implementation
Our lab has done past research on multi-agent navigation using Sequential Trajectory Planning (STP). This method assigns an order to each agent. The first agent determines its desired trajectory, then reports this trajectory to the second agent. The second agent view the first trajectory as a moving obstacle, then determines its trajectory. This process continues until all systems are accounted for. This is very similar to how current air traffic control works. However, this assumes that all agents can determine their trajectories offline and execute them perfectly online. If sudden changes come up, they have no method of replanning quickly. We are introducing FaSTrack into this project to allow for multi-agent navigation with fast replanning.
Interactions with humans
We are working to extend our multi-agent implementation to handling uncertain moving obstacles. Once we do this, we can use research on human-robot interaction to understand predictions about how humans navigate through environments. By making predictions about where a human might move, we can formulate this cone of possible trajectories as a moving obstacle to avoid. If the human makes sudden changes to their trajectory, FaSTrack will allow for quick replanning to remain safe.
Incorporating insight from humans
In our Meta-FaSTrack work we using inspiration from human cognitive models of "fast and slow" thinking. We would like to continue to explore the area of cognitive science to improve our navigation algorithms for efficiency and better human-robot interaction.
Uncertainty in the tracking model
FaSTrack assumes that the tracking system is essentially a perfect model of the true autonomous system (i.e. only bounded parametric uncertainty). However, this isn't always the case. If we find out that the structure of our tracking model is fundamentally wrong (e.g. change of basis in the state space, change in dimensionality, change in general structure of the dynamics model), can we efficiently update the tracking error bound?
If you have more ideas or thoughts please don't hesitate to contact me!
Related papers
[1] Sylvia Herbert*, Mo Chen*, SooJean Han, Somil Bansal, Jaime F. Fisac, and Claire J .Tomlin, "FaSTrack: a Modular Framework for Fast and Guaranteed Safe Motion Planning." IEEE Conference on Decision and Control, 2017. cite
[2] David Fridovich-Keil*, Sylvia Herbert*, Jaime F. Fisac*, Sampada Deglurkar, and Claire J .Tomlin, "Planning, Fast and Slow: A Framework for Adaptive Real-Time Safe Trajectory Planning." IEEE Conference on Robotics and Automation, 2018 (submitted). cite